Using Transformer Intervention to Increase Compositionality in Small Language Models
Adapted From a Project for Stanford CS224N: Natural Language Processing
Alex Warstadt, Leshem Choshen, Aaron Mueller, Adina Williams, Ethan Wilcox, and Chengxu Zhuang. Call for papers - the babylm challenge: Sample-efficient pretraining on a developmen- tally plausible corpus, 2023.
To address the BabyLM challenge, this study investigates whether increasing the compositionality of transformer models improves a model's ability to understand linguistic structure. Specifically, this study addresses the following questions:
- Question 1: How do transformer models behave when they are trained on small datasets, (as inspired by the limitations of human development)?
- Question 2: How can we measure the compositional understanding of these transformer models?
- Question 3: How can we encourage transformers to learn compositional representations of inputs to enhance their ability to generalize?
- Question 4: Do these compositional representations improve the model's ability to generalize?
Background: Tree Based Composition
The basic idea behind compositionality is that the meaning of a sentence is derived from the meaning of its parts and the way in which they are combined. For example, the meaning of the sentence "Red apples are delicious" can be broken down into the smaller sub-phrases "Red apples" and "are delicious", both of which have their own meanings (which can further be broken down, etc.). This sort of hierarchical composition is often represented using tree-based linguistic structures, which have been shown to be a common way for humans to understand language and have been correlated with increased compositional generalization in models (Murty et al., 2022). In a recent paper, Murty et al. introduced a novel metric, \( \mathbf{t_{\text{score}}} \), to measure how tree-structured a transformer model is. Using this metric, they demonstrated a correlation between a high \( \mathbf{t_{\text{score}}} \) (indicating tree-structuredness) and increased compositional generalization in transformer models. This metric is defined as follows: \[ t_{\text{score}} \triangleq \frac{1}{|\mathcal{D}|} \sum_{S \in \mathcal{D}} \left( \mathbb{E}_{T} \left[ \operatorname{SCI}(S, T) \right] - \operatorname{SCI}\left( S, \widehat{T}_{\text{proj}}(S) \right) \right). \] While it looks complicated, the purpose of this function is relatively simply, it searches for the optimal bracketing of an input sentence that maximizes the span contextual invariance (SCI) of each bracket. By maximizing the SCI of each of the sub-phrases, the function is finding the most optimal place in the sentence to split the words while maintaining chunks of text that have intrinsic meaning (for example, a bad bracketing of "red apples are delicious" would be "red apples are" and "delicious" because the phrase "red apples are" is not an independent clause with intrinsic meaning). By using a similarity function to measure how similar the embedding of the bracketed sentence is to the original sentence embedding, we can determine a relative score for how effective the transformer is at learning heierarchical composition. A visual representation of a tranformer comparing a bracketed embedding to the original embedding can be seen in Figure 2 below.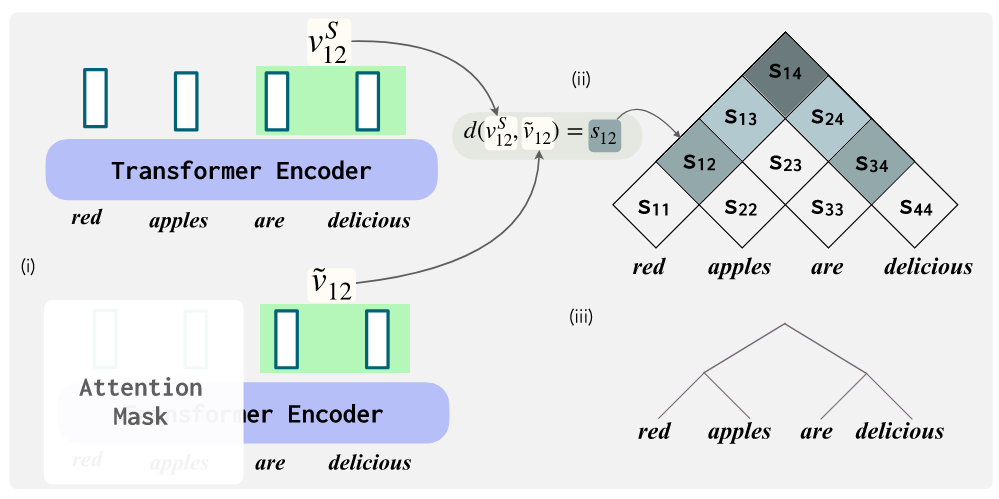
Shikhar Murty, Pratyusha Sharma, Jacob Andreas, and Christopher D. Manning. Characterizing intrinsic compositionality in transformers with tree projections, 2022.
Approach
In order to investigate the potential benefits of incorporating tree-structured computations into the transformer architectures, the study was split into a series of systematic steps. The detailed process for this study includes the following steps:- Step 1 | Baseline Language Model: Train GPT2-small architectures (6 and 12 encoder layers) on the dataset (10M tokens) provided by the BabyLM Challenge.
- Step 2 | Model Evaluation: Evaluate perplexity and run syntactic evaluations on BLiMP[1] to evaluate the models on common grammatical phenomena in English.
- Step 3 | Measure Tree-Structuredness: Incorporate the \( t_{\text{score}} \) metric into the GPT2 transformer architecture to measure tree-structuredness during training.
- Step 4 | Encouraging Tree-Structured Computations: Replace the cross-entropy loss \( \mathcal{L}_{\text{entropy}} \) of GPT-2 by a regularized loss: \( \mathcal{L}_{\text{entropy}} + \lambda \mathcal{L}_{\text{tree}} \) to encourage the transformer to learn tree-structured representations of inputs.
- Step 5 | Re-evaluate the Model: Re-evaluate the model using the same metrics as in Step 2.
Experimental Results
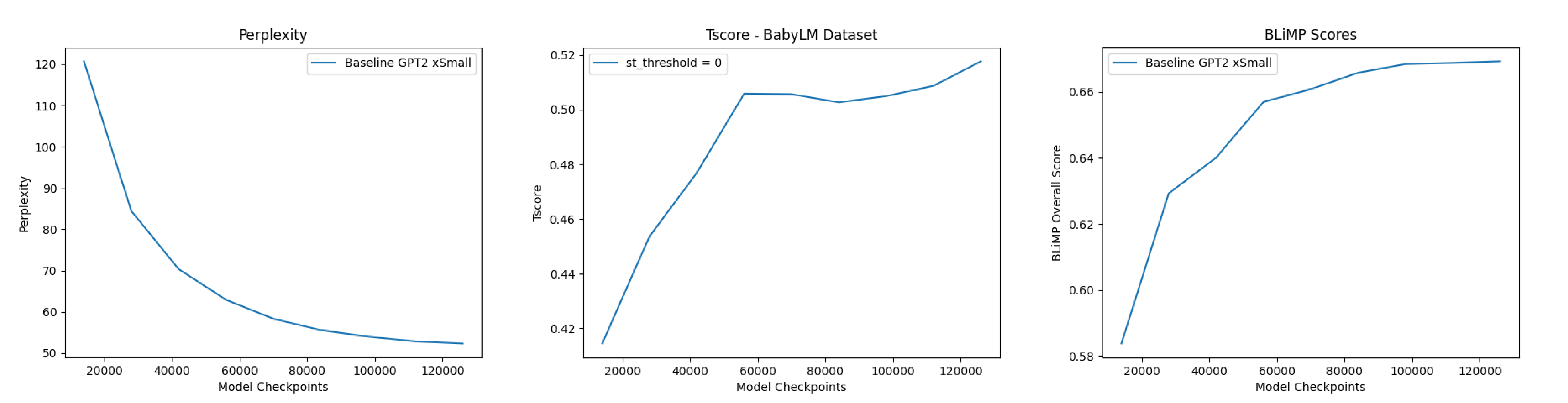
To begin this study, the two baseline GPT2 architectures described above were evaluated (6 and 12 layer versions). The difference in performance was found to be very minor, so moved forward using only the 6-layer encoder model for increased iteration speed. We then measured the model performance on perplexity, which can be seen in Figure 3 and found it to decrease as the model trained (indicating increasing ability of the model to correctly predict future tokens). Next, we ran a ensemble of syntactic evaluations using BLiMP (the Benchmark of Linguistic Minimal Pairs) framework (Warstadt et al., 2020), the scores of which can be seen in Table 1 below.| Model | BLiMP Overall Score |
|---|---|
| GPT2-BabyLM-Baseline | 0.69 |
| GPT2-Pretrained | 0.83 |
| Human Performance | 0.89 |
Table 1. BLiMP Scores
BLiMP scores tests the model's ability to discern a grammatically incorrect sentence from a pair of sentences (one correct, one incorrect), making the random chance score equal to 50%. Additionally, the model \( t_{\text{score}} \) was calculated at several points during training and showed an increase in tree-structuredness as training progressed and model performance increased. This mirrors the correlation described by Murty et al. (2022), but still does not indicate causation.
Figure 3. Baseline Model Results
Discussion
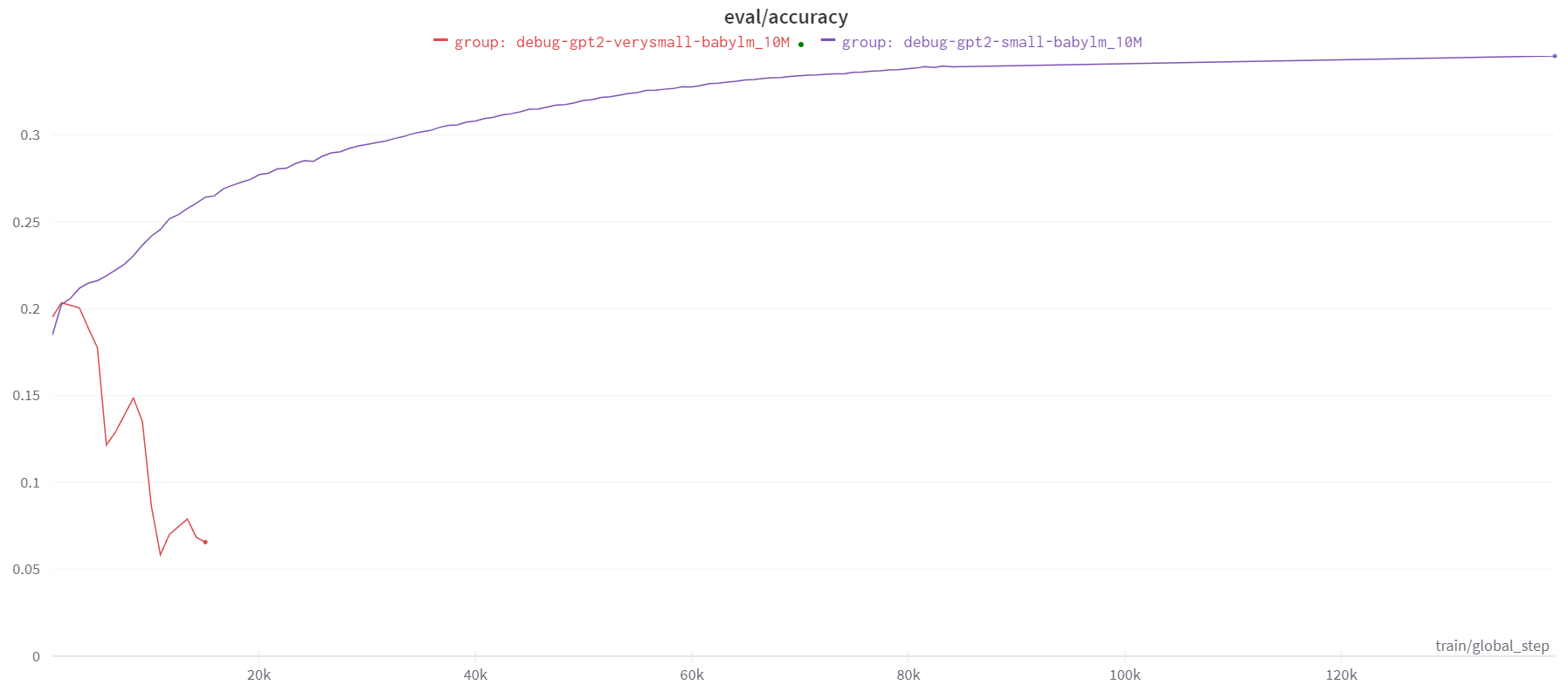
Finally, the updated GPT2 architecture with a tree-regularizing loss function was retrained on the same data as the baseline model. Its evaluation accuracy is plotted in orange below against the 6 layer encoder baseline model. Perplexity, BLiMP score, and \( t_{\text{score}} \) plots are omitted in this section as they show stochastic behavior similar to that seen in Figure 4 below and do not provide further insight into the behavior of the model.Astute observers may notice that the following figure does not describe a successful improvement in model performance. Even more astute observers may notice that the tree-regularized model was trained on far fewer epochs than the baseline model. The reason for both of these facts is simple: the tree-regularized model we trained was bad. It should be noted that the underlying principles propelling these tests are not inherently flawed, instead the issues likely arose from limiting factors imposed on our implementations.
Figure 4. Evaluation Accuracy
By checking the \( t_{\text{score}} \) of the model at various checkpoints, we can see that the model was learning to produce more tree-structured outputs. However, it is clear from the evaluation accuracies that this did not result in improved model performance. It is likely that the regularization factor \( \lambda \) was too large, leading the model to overfit on the tree-structuredness of the training data. Despite running the model with several different values of \( \lambda \), we were unable to find a value that resulted in improved model performance. The challenge with iterating on this variable stems form the algorithmic runtime of the recursive chart parsing used to calculate \( \mathcal{L}_{\text{tree}} \). The time complexity for this function is \(O(n^3) \), where \(n\) is related to the length of the input sequence as well as the number of input sentences analyzed per batch. Unfortunately, this means that the runtime of the model is incredibly slow. In attempts to reduce this runtime, we made additional simplifications that would speed up the calculations but would likely have a negative impact on model performance. The two main simplifications we made were truncating all input sentences to a maximum of 10 words and set our maximum sentence batch size to 50. A future goal of this study would be to quantify the impact of these assumptions by running the model with increasing words and batch sizes, as it is currently unknown how heavily this impacts the model performance (although I believe this impact to be significant).
Both of these assumptions likely have very large impacts on model performance, as they increased the inherent stochasticity in the gradient updates, since each update is based on a very small percentage of the overall dataset. Accounting for the fact that our training dataset contained 650,000 input sentences, a batch size of 50 is only 0.008 percent of the overall dataset. We attempted using 1 percent of the overall dataset to calculate \( \mathcal{L}_{\text{tree}} \) at each step, however, training was estimated to take over 600 hours (again due to the \(O(n^3)\) runtime).
Future Work
Since it is clear from these tests that the model overfit to the tree-structuredness of the training data, it would be interesting to see how the model performs if we scaled up the regularization factor \( \lambda \) during training. If we started with a value of zero and slowly increased it over time, it may allow the model to learn a more comprehensive understanding of language before imposing the tree-structured constraint. This may result in a more robust model that is able to construct a more compositional understanding of language. Another drawback to the viability of this approach is its algorithmic runtime of the tree-regularizing loss function. As it is currently, using this method (even for small-scale datasets) presents challenges for individuals wishing to train models. It is possible to reduce the runtime to at least \(O(n^2)\), which would increase the feasibility of using this method, and would likely result in improvements over the performance seen in this study. Hopefully this avenue is explored in the future so that further research can be conducted on the impact of imposed tree-structured computations in transformer models and their abilities to gain increased compositional generalization without the need for massive training corpuses.References
[1] Shikhar Murty, Pratyusha Sharma, Jacob Andreas, and Christopher D. Manning. Characterizing intrinsic compositionality in transformers with tree projections, 2022.[2] Alex Warstadt, Leshem Choshen, Aaron Mueller, Adina Williams, Ethan Wilcox, and Chengxu Zhuang. Call for papers - the babylm challenge: Sample-efficient pretraining on a developmentally plausible corpus, 2023.
[3] Alex Warstadt, Alicia Parrish, Haokun Liu, Anhad Mohananey, Wei Peng, Sheng-Fu Wang, and Samuel R. Bowman. Blimp: The benchmark of linguistic minimal pairs for english. Transactions of the Association for Computational Linguistics, 8:377-392, 2020.