Nonlinear Structural Analysis of Rocking CLT Shear Walls
Adapted From a Project for Stanford CEE282: Nonlinear Structural Analysis
Introduction
As buildings continue to escalate in height and complexity, earthquakes have caused increased damage and economic hardships in the built environment. This, paired with an increasing desire to depart from life-safety based design, stresses the need for engineers to design seismically resilient buildings. Post-tensioned (PT) rocking walls are one way this can be accomplished. PT rocking walls allow for controlled uplift to occur during a seismic event which creates a rocking motion. This rocking behavior has a substantial impact on the behavior of the lateral system. It reduces the reaction forces, increases the natural period, and increases the lateral displacements. As a system, PT rocking walls have been extensively studied for both concrete and steel; however, cross laminated timber (CLT) is a relatively new material (especially in the United States) and is far less researched, demanding the need for further study.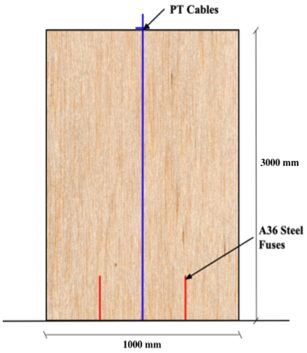 CLT is an emerging structural
material, it is composed of layers of timber glued together in an
orthogonal configuration. This layout allows for CLT to have high
strength, rigidity, and two-way span capacity. These traits allow
for CLT to be a comparable structural material to steel and
concrete. CLT has only been used in the United States since the
early 2000s; therefore, the design code requirements are not as
exhaustive as the requirements for concrete and steel.
CLT is an emerging structural
material, it is composed of layers of timber glued together in an
orthogonal configuration. This layout allows for CLT to have high
strength, rigidity, and two-way span capacity. These traits allow
for CLT to be a comparable structural material to steel and
concrete. CLT has only been used in the United States since the
early 2000s; therefore, the design code requirements are not as
exhaustive as the requirements for concrete and steel.
The system being studied in this research project is depicted in Figure 1. The three main components of PT rocking walls are as follows. (1) The CLT shear wall which allows for transfer of gravity and lateral forces. (2) The vertical PT cable which allows for self centering to occur, creating a more resilient system; however, if the PT cable were to yield it would result in large residual drifts for the system. (3) The A36 steel fuses serve to dissipate the energy of the system.
This paper focuses on the effect of CLT toe crushing on the global response of the PT rocking wall system. Toe crushing is a relatively unique characteristic to timber walls; it is a phenomenon in which the extreme fibers of the wall experience crushing at low stresses. This research project involves the creation of a computational model of a PT CLT rocking wall and verification of the model using data from a previous research paper (Chen). The model will be used to study the effect of ground motions on CLT toe crushing.
Modeling Assumptions
To facilitate this study's goal of observing the effects of toe crushing behavior, two models were created in SAP2000, one in which toe crushing was explicitly modeled and one in which it was neglected. Figure 2 depicts the base of the modeled CLT rocking wall and indicates some of the key model parameters (see the appendix for a full view of the SAP model). Springs (K1) were used to capture the effects of localized toe crushing in the CLT wall.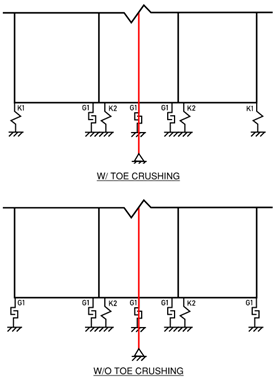 These toe springs were modeled as bilinear plastic compression
elements and have a post yielding increase in stiffness to account
for the densification of the wood as it crushes. A previous research
study provided a baseline for the toe crushing parameters used to
model this element (Jin), however the provided values were adjusted
within 10 percent to more closely match the model behavior with
results from physical testing (Chen) (see the appendix for the
spring parameters used in this SAP model). This 10 percent
adjustment was to account for differences in wood properties in the
CLT used by both the physical testing done by Chen and the CLT
parameters published by Jin. Modeling the toe springs as bilinear
elements is a very coarse assumption and led to minor inaccuracies
in the model (further discussed in the Verification section).
Further extrapolation beyond this simplified assumption is possible,
however, it was a research avenue that this project chose not focus
on due to a lack of verification data.
These toe springs were modeled as bilinear plastic compression
elements and have a post yielding increase in stiffness to account
for the densification of the wood as it crushes. A previous research
study provided a baseline for the toe crushing parameters used to
model this element (Jin), however the provided values were adjusted
within 10 percent to more closely match the model behavior with
results from physical testing (Chen) (see the appendix for the
spring parameters used in this SAP model). This 10 percent
adjustment was to account for differences in wood properties in the
CLT used by both the physical testing done by Chen and the CLT
parameters published by Jin. Modeling the toe springs as bilinear
elements is a very coarse assumption and led to minor inaccuracies
in the model (further discussed in the Verification section).
Further extrapolation beyond this simplified assumption is possible,
however, it was a research avenue that this project chose not focus
on due to a lack of verification data.
Additionally, at the base of the wall, gap (or contact) elements (G1), were used to provide compression only support. This in turn allows for the wall to exhibit its characteristic rocking behavior. These elements were only used in the middle three nodes; however, the model without toe crushing also used these elements at the ends of the wall instead of the springs used to model toe crushing. This allows for the model without toe crushing to rock freely without considering toe crushing. Furthermore, another spring element (K2) was used to model the fuses (or hold downs). These elements were located at the inner third points and serve to represent the buckling restrained A36 steel fuse rods that act as an energy dissipation mechanism for the system. These elements were modeled as multilinear springs which means there was a detailed backbone curve. SAP2000 has significantly more information on A36 steel than it does CLT which is why the fuses could be modeled as multilinear while the toe crushing elements were modeled as bilinear. Finally, the post tensioning cable is anchored below the base of the wall. This was done to ensure there is no unrealistic fixity at that middle node due to a pinned support. Figure 2 depicts a greatly exaggerated location of the post tensioning anchor location for visual purposes. The actual model has the anchor just below the other modeled elements.
Model Verification
After the model was completed, a research paper was used to verify the model results. Figure 3 shows results from the model completed for this study on the left as well as results from the research paper (Chen) on the right and shows force vs. displacement curves under monotonic loading with differing post-tensioning forces. Additionally, Figure 4 shows the same results under cyclic loading rather than monotonic.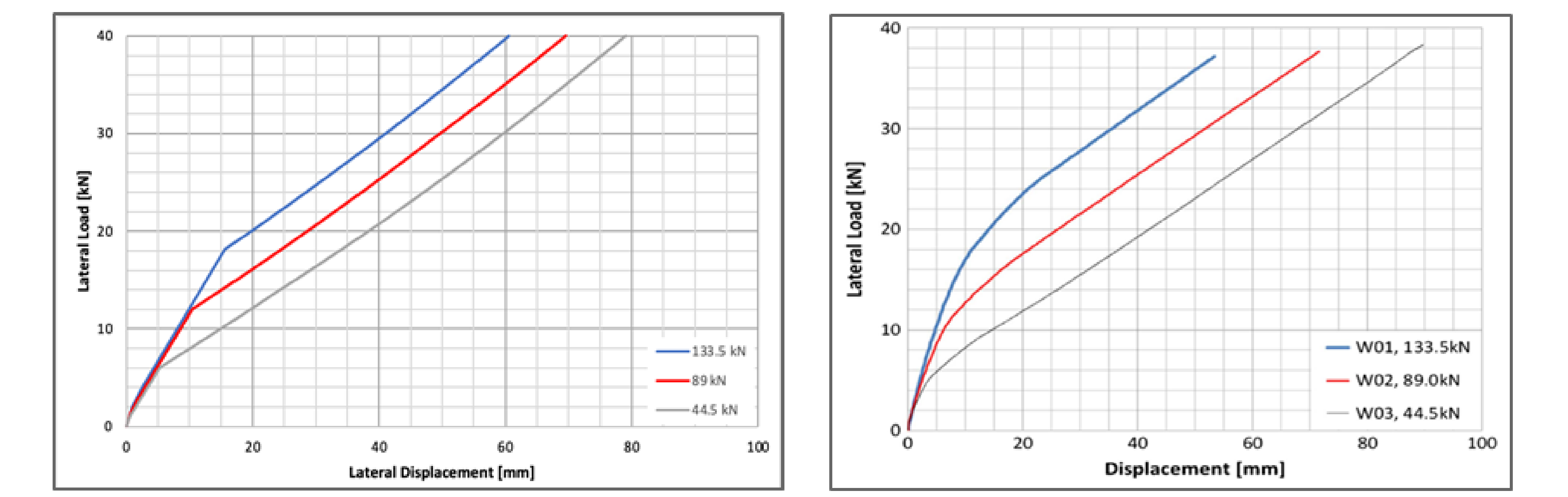
Figure 3: Force vs. Displacement under Monotonic Loading With Toe Crushing
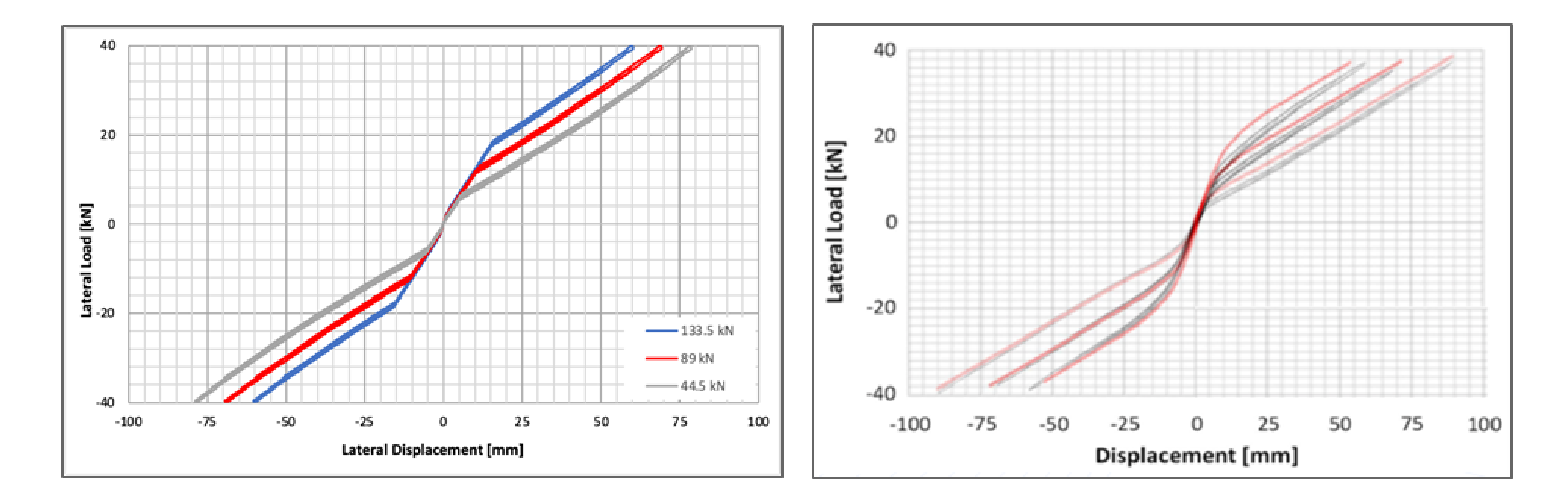
Figure 4: Force vs. Displacement under Cyclic Loading With Toe Crushing
A visual inspection of Figure 3 indicates a close match between this study's results and the results from previous, physical testing. Closer analysis of the two graphs show that both the pre and post-crushing stiffnesses are relatively well captured in this model, as well as the point of crushing (shown by the transition between the two slopes). The force and displacement at crushing match closely between the two graphs, however, the curvature shown in the physical test is not represented in the SAP model, a result of the bilinear nature of the CLT toe springs used. The main difference between the two graphs is the magnitude of displacements. The SAP model was calibrated using a post-tensioning force of 89 kN (shown as the red line) and as a result, the displacements corresponding to this loading condition match very closely with the physical testing. However, for the other two load cases (44.5 kN and 133.5 kN), the displacements are less accurate, falling within 10 percent of the physical test values. Furthermore, Figure 4 displays both the same similarities and discrepancies seen in Figure 3. It should be noted that the physical testing report displayed results in a series of three separate graphs, for ease of comparison these graphs were overlaid and displayed together. The hysteresis loops correspond to the same order of appearance as the hysteresis loops displayed in this study's results. Overall, these slight differences were likely due to the simplifications present in the CLT toe spring modeling assumptions. As both the pre and post-yielding stiffnesses are relatively similar, the differences in ultimate deflection are likely a result of the toe springs yielding at the incorrect point, although as there is no clear yield point in the physical testing, this is difficult to accurately diagnose.
To further verify the accuracy of the model, hysteresis loops were plotted in Figure 5 for the SAP model with toe crushing explicitly modeled. Additionally, Figure 6 shows the hysteresis loop for the SAP model without toe crushing modeled.
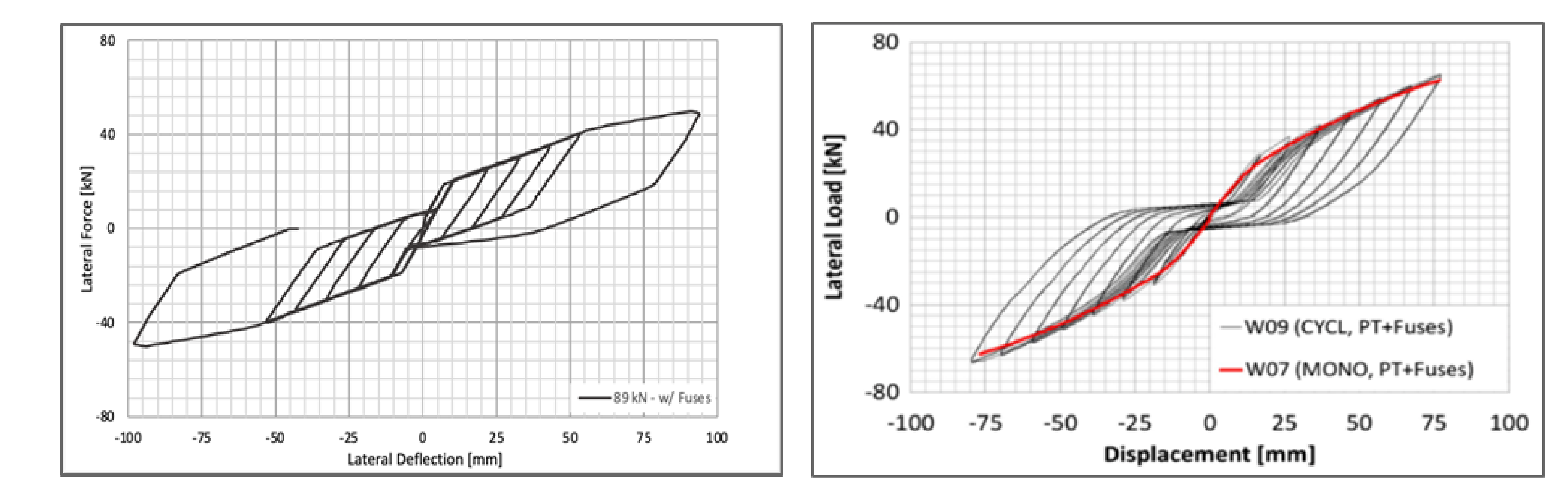
Figure 5: Force vs. Displacement under Cyclic Loading With Toe Crushing and A36 Hold-downs
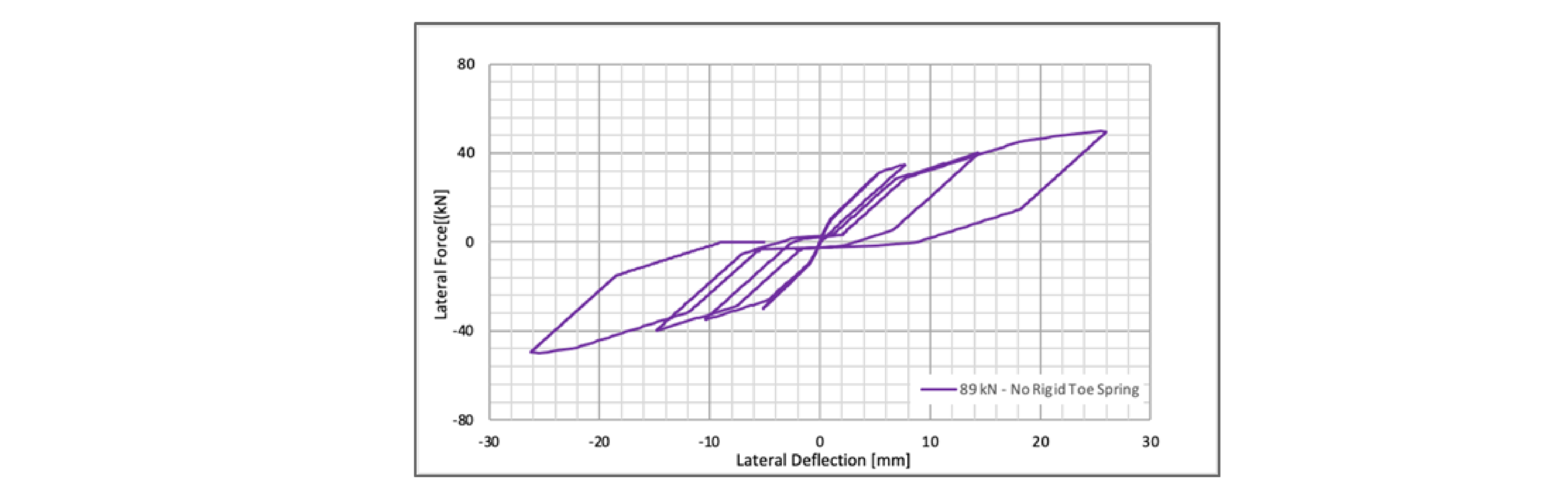
Figure 6: Force vs. Displacement under Cyclic Loading With A36 Hold-downs and No Toe Crushing
Despite not having a direct comparison, Figure 6 serves to assess the validity of this project's assumptions. One of the key features Figure 6 illustrates is the general shape of the hysteretic curve, with one of the major components being the distinct flag-shape that is commonly seen with rocking systems. Additionally, this graph shows an unloading response much closer to that of the physical test. The deflections presented by this figure, however, do not match the physical test, as this figure reflects a model with no toe crushing. By assessing these features, it was confirmed that all gap elements were correctly allowing the shear wall to rock, and the steel hold-down rods were dissipating energy as expected. Looking at Figure 5 a similar flag shape can be seen, however, the main difference is in the unloading phases. The toe-crushing model in Figure 5 exhibits a linear-elastic unloading phase for the majority of the loop which contrasts what is seen in Figure 6. One likely cause could be that the yield stress of the CLT used in this SAP model is too high, restricting it from entering its post-crushing behavior. Unfortunately, it was unclear what CLT properties were used in the physical testing so this is a likely area for uncertainty in this study. Overall, the general shape and deflection values are similar enough in Figure 5 to conclude that this model provides reasonable accuracy in predicting the behavior of a post-tensioned CLT rocking shear wall.
Additional model parameters were adjusted to ensure realistic responses in SAP, however, the following parameters were deemed insignificant to the global behavior of the system. The mesh size of the shear wall elements (modeled as shell elements with CLT material properties) was reduced to 100-millimeter squares. This greatly increased computation time but had no significant effect on deflections or reaction forces. Additionally, the lateral support conditions of the wall were analyzed. The shear wall is laterally supported at each of the toes, however, under large rocking deformations there is a potential for this to result in unrealistic tensile reaction forces at each of these locations. To eliminate these unrealistic reactions, gap elements were used in place of rigid lateral restraints to provide compression-only supports. It was found that these lateral gap elements increased computation time and provided no significant changes in global response, so typical lateral restraints were used.
Testing and Results
After verifying that this SAP model was able to replicate the results from physical testing conducted by Chen, two direct-integration time history analyses were run to assess the performance of a CLT rocking shear wall under ground motions. The ground motions used in these analyses were scaled according to the model with toe crushing and were adjusted so that the maximum base shear felt by the wall was the same as its design load (approximately 20 kN). This was then scaled up to three times the design load (or about 60 kN) to evaluate performance at loads that were much higher than the design level. Two ground motions, Array 06 and Lucerne, were selected from the SAP2000 time history database.After the ground motions were scaled, they were run through both SAP models (with and without toe crushing) to evaluate the change in performance due to the crushing phenomenon. The results of these tests can be seen in Table 1.
| With CLT Toe Crushing | Without CLT Toe Crushing | |||||||
|---|---|---|---|---|---|---|---|---|
| GMM | GM 1* | GM 2* | GM 1 | GM 2 | GM 1 | GM 2 | GM 1 | GM 2 |
| Scale | Scale 1 (Design Load) |
Scale 2 (Design Load x Ω) |
Scale 1 | Scale 2 | ||||
| Base Shear (kN) | 23 | 22 | 63 | 60 | 18 | 33 | 88 | 102 |
| Max Displacement (mm) | 8.2 | 6.6 | 132 | 53 | 3.0 | 3.75 | 42.1 | 32.4 |
| Residual Displacement (mm) | 0.6 | 0.3 | 1.4 | 1.0 | 0.00 | 0.00 | 0.15 | 0.16 |
| Max CLT Toe Crushing | 0.5 | 0.7 | 11.5 | 5.4 | - | - | - | - |
*GM 1 - ARRAY 06 (SAP2000)
*GM 2 - LUNCERNE (SAP2000)
The results clearly show a significant difference when toe crushing is accounted for. Firstly, the residual drift decreased when toe crushing was not accounted for; however, since it was not extremely large in the toe crushing model, this decrease is not a highly significant effect. More importantly, the maximum displacement significantly decreased, while the max base shear drastically increased. This is consistent with research surrounding rocking shear walls; it is often observed that the more the wall is allowed to rock, the lower the base shear and other support reactions are (Anderson). Finally, It should be noted that throughout all of these tests, the post-tensioned cable that provides the self-centering was kept to approximately 60 percent of its yield stress, so the residual drifts were not due to this tendon yielding.
Conclusion
Several conclusions can be drawn from the results of this research project. Firstly, toe crushing was found to significantly increase the maximum lateral wall drift. This is a realistic result when considering the global behavior of the system. Figure 7 shows an exaggerated model that infers how crushing at the toes can produce larger rocking effects and thus increase lateral drift.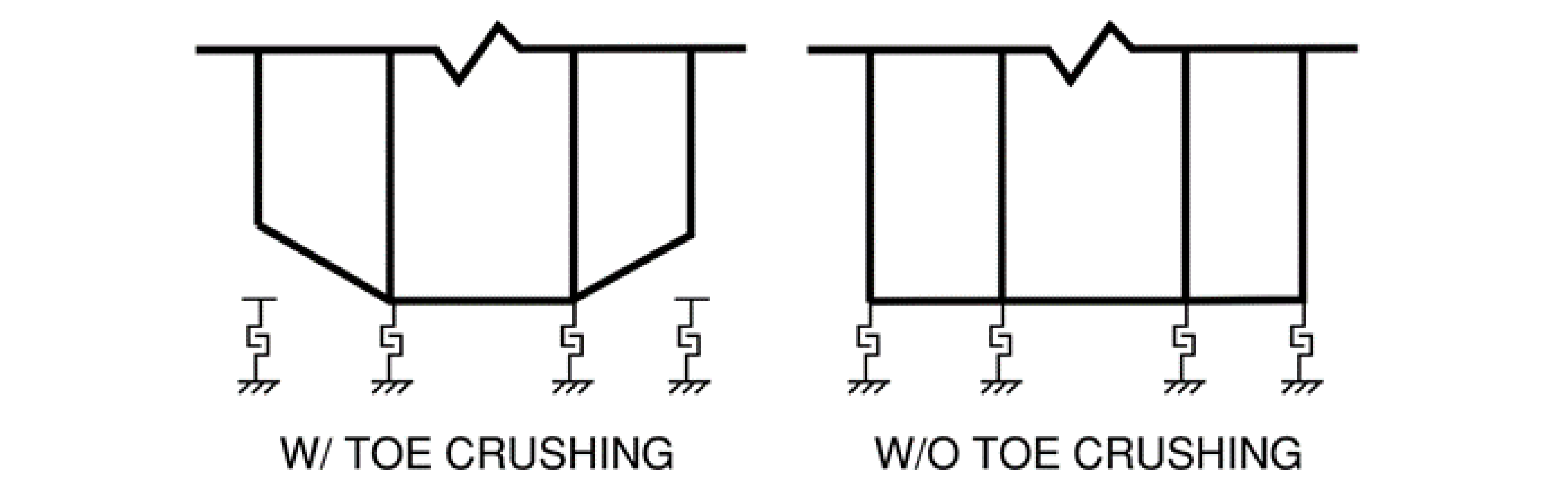
Figure 7: Simplified Visual Description of Wall With Toe Crushing (left) and Without Toe Crushing (right)
Additionally, the increased drift caused by toe crushing was also found to significantly decrease the reaction forces, which matches typical rocking frame behavior (Anderson). Finally, the residual drift is minorly affected by toe crushing. This is likely due to the two following reasons. First, the self-centering of the wall is controlled by the post-tensioned cable and as the cable is kept well within its elastic region, there is little difference in its behavior between the model with toe crushing and the model without. Secondly, this model has rigid contact elements at the center nodes (seen in Figure 2); therefore, even if there is significant crushing in the toes, the behavior of the walls will be similar when there are small drifts and the wall is resting on the center nodes, as was the case at the ends of both applied ground motions (see Figure 7).
Real world applications can be drawn from these results. Based on this research, it is recommended that when analyzing rocking CLT shear walls, the effects of toe crushing should be explicitly modeled as it has significant impacts on the behavior of the system. Modeling without accounting for toe crushing will result in grossly underestimated drifts and overestimated reaction forces.
Future Study
Several research avenues have been disregarded over the course of this project in the interest of maintaining a well-defined scope. One such avenue is to look into further discretization of the model and add more crushing springs along the length of the wall rather than providing central support with rigid gap elements, as is currently modeled. Whether or not this would be an accurate description of the real behavior of the wall would need to be verified, but it would provide continued research opportunities.References
Amini, M. Omar, et al. “Rocking Behavior of High-Aspect-Ratio Cross-Laminated Timber Shear Walls: Experimental and Numerical Investigation.” Journal of Architectural Engineering, vol. 27, no. 3, 2021, https://doi.org/10.1061/(asce)ae.1943-5568.0000473.Anderson, D. L. (n.d.). Effect of foundation rocking on the seismic response of shear walls. Retrieved from https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.549.9615&rep=rep1&type=pdf.
Chen, Zhiyong, et al. “Structural Performance of Post-Tensioned CLT Shear Walls with Energy Dissipators.” Journal of Structural Engineering, vol. 146, no. 4, 2020, p. 04020035., https://doi.org/10.1061/(asce)st.1943-541x.0002569.
Eatherton, Matthew, et al. “Seismic Design and Behavior of Steel Frames with Controlled Rocking—Part I: Concepts and Quasi-Static Subassembly Testing.” Structures Congress 2010, 2010, https://doi.org/10.1061/41130(369)138.
Jin, Z., et al. “Simplified Mechanistic Model for Seismic Response Prediction of Coupled Cross-Laminated Timber Rocking Walls.” Journal of Structural Engineering, vol. 145, no. 2, 2019, p. 04018253., https://doi.org/10.1061/(asce)st.1943-541x.0002265.
Appendix
Appendix A: Toe Crushing Spring Properties:
- The toe-crushing springs were modeled as bilinear plastic link elements
- Initial Stiffness: 29.42 kN/mm
- Post-yielding stiffness: 0.8262 kN/mm
- Yielding Force: 0.1644 kN
- Kinematic hardening was assumed
- The following is the hysteretic backbone curve used for toe-crushing springs:
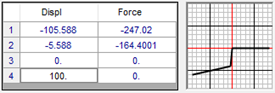
Appendix B: Hold-down Spring Properties:
- A36 hold-down springs were modeled as multilinear plastic link elements
- Kinematic hardening was assumed
- The SAP2000 default A36 steel material backbone curve was used
